EM（期望最大化）

EM算法是包含隐藏变量的极大似然估计算法。

它涉及到迭代交替求解对数似然函数的期望和最大化似然的参数。

常见的应用包括拟合混合模型、包含潜在参数的贝叶斯网络和隐马尔可夫模型。

1.Jensen不等式

定理：

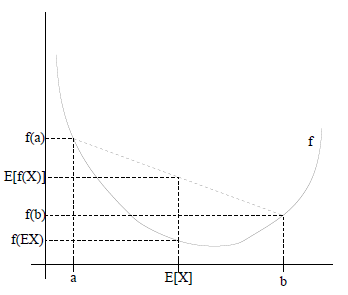
如果$f$是凸函数，$X$是随机变量，那么

如果$f$是严格凸的，那么$E[f(X)]=f(EX)$成立，当且仅当$X=E[X]$的概率为100%，也就是说X是一个常量。

这里把$f(E[X])$简写成$f(EX)$。

如下图所示，实线$f$是一个凸函数，有0.5概率是a，0.5的概率是b（就像抛硬币一样）。$X$的期望就是a和b的中值。

Jensen不等式应用于凹函数时，不等号方向相反，$E[f(x)] \leq f(EX)$

2.EM算法

给定一个包含$m$个样本的训练集{ $x^{(i)}, x^{(2)}, ... , x^{(m)}$ }，样本间相互独立，我们想知道每个样本隐含的类别z，能使得$p(x,z)$最大的$\theta$，其中$p(x;\theta)$的似然函数如下：

第一步是对极大似然取对数，将求积变成求和；第二步是对每个样本的每种类别$z$求联合分布概率和。但是直接求解$\theta$是很困难的，因为这里有一个潜在随机变量$z^{(i)}$。一旦$z^{(i)}$确定了，求解就容易了。

在这种情况下，EM算法给出了一个有效的求解极大似然估计的方法。直接最大化$l(\theta)$很困难，EM的策略是，反复地构造$l$的下界(E-step)，然后最优化这个下界(M-step)。

对于每一个样例$i$，用$Q_i$表示该样例隐含变量$z$的某种分布，$Q_i$满足的条件是，$\sum_z{Q_i(z)}=1$，$Q_i(z)\geq0$。（如果z是连续性的，那么$Q_i$是概率密度函数，需要将求和符号换做积分符号）。比如，要将班上学生聚类，假设隐藏变量$z$是身高，那么就是连续的高斯分布。如果按照隐藏变量是男女，那么就是伯努利分布了。

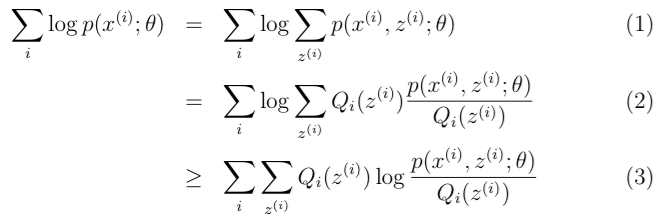
(2)到(3)运用了Jensen不等式，$f(x)=\log x$是凹函数（$f''(x)=-1/{x^2}$，在$x\in R^+$的定义域里永远为负数）